Modelagem Multinível
GLMM - Generalized Linear Models Multilevel
- Modelos multinível
- Modelos hierárquicos
- HLM (Hierarchical Linear Models)
- Mixed Models
- GLLAMM (Generalized Linear Latent and Mixed Models)
- Nested Models (Modelos Aninhados)
- Modelos Contextuais
- RCM (Random Coefficient Models)
Modelos Multinível
Modelos multinível são modelos estatísticos que permitem a análise de dados hierárquicos, ou seja, dados que possuem uma estrutura de aninhamento, como por exemplo, alunos em escolas, pacientes em hospitais, funcionários em empresas, etc.

-
Y = efeito fixo + efeito aleatório + erro
-
Modelos multinível naturalmente consideram heterocedasticidade naturalmente. Diagnostico da heterocedasticidade (cone se abrindo) é omissão de variáveis relevantes, no caso de GLMM considera naturalmente pois considera efeitos aleatórios de inclinação e intercepto.
-
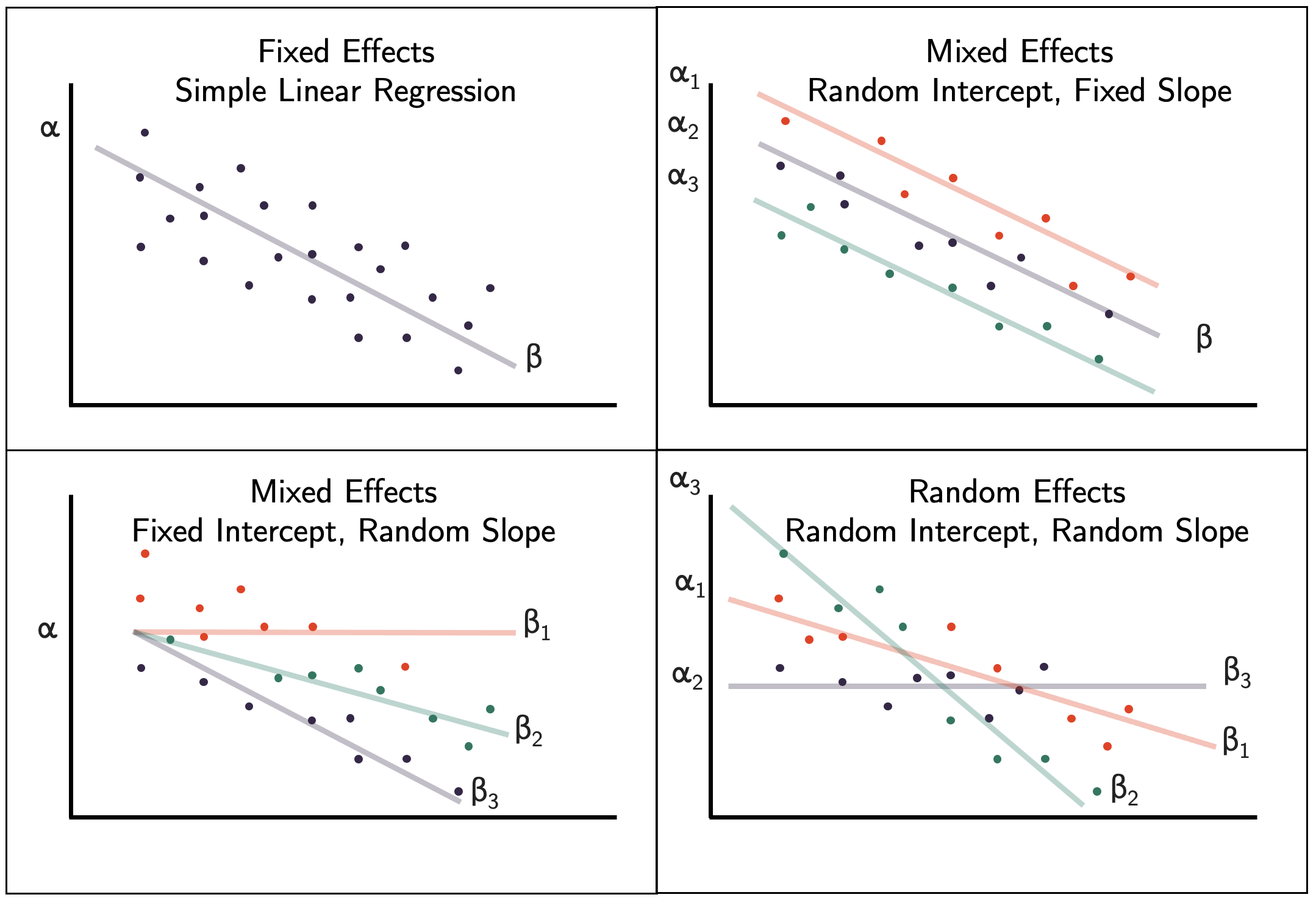
var(u_0j): Variância dos efeitos aleatórios de intercepto -
var(u_ij): Variância dos efeitos aleatórios de inclinação -
var(u_0j) ~= 0 e var(u_ij) ~= 0: OLS(GLM) -
var(u_0j) ~= 0 e var(u_ij) != 0: Interceptos aleatórios -
var(u_0j) != 0 e var(u_ij) ~= 0: Inclinações aleatórias -
var(u_0j) != 0 e var(u_ij) != 0: Interceptos e inclinações aleatórias
-
OLS é um caso especial de GLMM, onde não há efeitos aleatórios.
-
Dummização permite eventos aleatórios de intercepto.
-
Box-Cox Transformation - Transformação de Box-Cox é uma técnica que pode ser usada para estabilizar a variância e tornar os resíduos mais próximos da normalidade. As vezes nem isso é suficiente, e é necessário usar modelos multinível.
Se a variância dos termos aleatórios forem estadisticamente diferentes de zero, então o modelo multinível é mais apropriado.
-
Não existe procedimento stepwise para estimação de modelagem multinível, pois a retirada de uma variável pode afetar o modelo como um todo. Utiliza-se a estratégia de step-up.
-
ICC: Intraclass Correlation Coefficient - Mede a proporção da variância total que é devida a variação entre os grupos.
ICC = Variância entre os grupos / Variância total. Mostra o quanto da variância é explicada pelo efeito do grupo.
Step-Up Strategy
- Primeiro roda-se o modelo nulo (modelo sem variação no x, so tem efeito aleatório de intercepto), Se a variância do efeito aleatório de intercepto nao for estaticamente aleatório, nao se justifica a modelagem multinível, é OLS.
- nível 1:
desempenho_ij = β_0j + e_ij - nível 2:
β_0j = γ_00 + u_0j(γ_00 grand mean ou intercepto - componente de efeito fixo, u_0j efeito aleatório de intercepto) - substituindo:
desempenho_ij = γ_00 + u_0j + e_ij(se não tiver variação de u_0j, não se justifica a modelagem multinível)
- Modelo com intercepto e inclinação aleatórios.
- nível 1:
desempenho_ij = β_0j + β_1j * x_ij + e_ij- e_ij erro indiossincrático - nível 2:
β_0j = γ_00 + u_0jeβ_1j = γ_10 + u_1ju_0j efeito aleatório de intercepto, u_0j efeito aleatório de inclinação - substituindo:
desempenho_ij = γ_00 + γ_10 * x_ij + u_0j + u_1j * x_ij + e_ij-γ_00 + γ_10 * x_ijefeito fixo,u_0j + u_1j * x_ijefeito aleatório
- Modelo final
- nível 1:
desempenho_ij = β_0j + β_1j * x_ij + e_ij - nível 2:
β_0j = γ_00 + γ_01 * z_j + u_0jeβ_1j = γ_10 + γ_11 * z_j + u_1j - substituindo:
desempenho_ij = γ_00 + γ_01 * z_j + γ_10 * x_ij + γ_11 * z_j * x_ij + u_0j + u_1j * x_ij + e_ij
Desafios de Modelos Multinível
- Interações profundas e capacidade de processamento
- Métodos de estimação dos parâmetros
- Clusterização da amostra
Python code
re = random effects fe = fixed effects groups = agrupamento pela variável data = dataframe (bancos de dados)
Modelo Nulo
import statsmodels.api as sm
sm.MixedLM.from_formula('y ~ 1', data=df, groups='x1', re_formula='1').fit()
Modelo com Intercepto e Inclinação Aleatórios
import statsmodels.api as sm
sm.MixedLM.from_formula('y ~ x1 + x2', data=df, groups='x1', re_formula='x2').fit()
Modelo Final
import statsmodels.api as sm
sm.MixedLM.from_formula('y ~ x1 + x2 + x1:x2', data=df, groups='x1', re_formula='x2).fit()
- dois pontos (:): interação entre x1 e x2 (multiplicação)
Previsão
A função predict não considera os efeitos aleatórios de intercepto ou de inclinação por grupo. Neste sentido, precisamos adicioná-los a partir dos parâmetros do modelo.
O predict na modelagem multinível é considera apenas o componente de efeito fixo.
import statsmodels.api as sm
model = sm.MixedLM.from_formula('y ~ x1 + x2 + x1:x2', data=df, groups='x1', re_formula='x2).fit()
fixed_result = model.predict(pd.DataFrame({'x1': [123], 'x2': [456], 'group': ['A']}))
Adicionando os efeitos aleatórios:
re = pd.DataFrame(model.random_effects).T # T: matriz transposta
result = fixed_result + re['v0j'][0] * 123 + re['v1j'][0] * 456
# v0j e v1j são os efeitos aleatórios de intercepto e inclinação
# [0] é o índice do grupo A
Na Mão...
fitted_fixed = intercept + beta1 * x1 + beta2 * x2 + beta3 * x1 * x2
fitted_random = u0j + u1j * x1 + u2j * x2 + u3j * x1 * x2
fitted = fitted_fixed + fitted_random
beta3 = beta1:beta2
Modelagem HLM3 com medidas repetidas
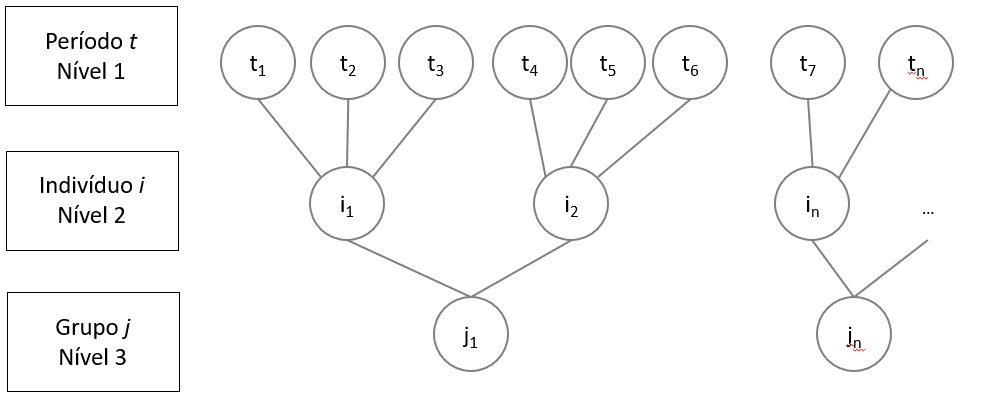
- Nivel 1: Período t (serie temporal)
- Nivel 2: Indivíduo j
- Nivel 3: Grupo k
- Modelos Nulo:
- nível 1:
desempenho_tjk = beta_0jk + erro_tjk(erro_tjk = erro indiossincrático) - nível 2:
beta_0jk = gamma_00k + u_0jk(efeito aleatório do indivíduo) - nível 3:
gamma_00k = delta_000 + tau_00k(delta_000 = grand mean, tau_00k = efeito aleatório do grupo) - substituindo:
desempenho_tjk = delta_000 + tau_00k + u_0jk + erro_tjk(delta_000 = EF, restante EA)
ICCs (Intra-Class Correlation): proporção da variância total que é devida a variância entre os grupos.
icc_grupo = var(tau_00k) / (var(tau_00k) + var(u_0jk) + var(erro_tjk)) icc_individuo = var(u_0jk) / (var(tau_00k) + var(u_0jk) + var(erro_tjk))
Obs: Na aula grupo = escola, individuo = aluno.
- Modelo com Intercepto e Inclinação Aleatórios
- nível 1:
desempenho_tjk = beta_0jk + beta_1jk * tempo_tjk + erro_tjk - nível 2:
beta_0jk = gamma_00k + u_0jkebeta_1jk = gamma_10k + u_1jk - nivel 3:
gamma_00k = delta_000 + tau_00kegamma_10k = delta_100 + tau_10k - substituindo:
desempenho_tjk = delta_000 + delta_100 * tempo_tjk + u_0jk + u_1jk * tempo_tjk + tau_00k + tau_10k * tempo_tjk + erro_tjk
- Modelo Final - Modelo de tendência linear com interceptos e inclinações aleatórios e as variáveis de ativ de nivel 2 e texp de nivel 3.
- nível 1:
desempenho_tjk = beta_0jk + beta_1jk * tempo_tjk + erro_tjk - nível 2:
beta_0jk = gamma_00k + gamma_01k * ativ_jk + u_0jkebeta_1jk = gamma_10k + gamma_11k * ativ_jk + u_1jk - nivel 3:
gamma_00k = delta_000 + delta_001 * texp_k + tau_00kegamma_01k = delta_010egamma_10k = delta_100 + delta_101 * texp_k + tau_10kegamma_11k = delta_110 - substituindo:
desempenho_tjk = delta_000 + delta_100 * tempo_jk + delta_010 * ativ_jk + delta_001 * texp_k + delta_110 * ativ_jk * tempo_jk + delta_101 * texp_k * tempo_jk + u_0jk + u_1jk * tempo_jk + tau_00k + tau_10k * tempo_jk + erro_tjk
Python
- Modelo Nulo
import statsmodels.api as sm
modelo_nulo_hlm3 = sm.MixedLM.from_formula("desempenho ~ 1", data=df, groups=df["grupo"], re_formula="1", vc_formula={"individuo": "0 + C(individuo)"})
- desempenho: variável dependente
- re_formula: efeito aleatório do indivíduo
- vc_formula: componente de variância do grupo
A função mixedlm() não comporta efeitos aleatorios de inclinação para os niveis 2 e 3 simultaneamente. Para isso, é necessário usar a função Lmer() do pacote pymer4.models.
from pymer4.models import Lmer
modelo_nulo_hlm3 = Lmer(formula="desempenho ~ 1 + (1|grupo) + (1|individuo)", data=df)
md_nulo_hlm3.fit()
- Modelo com Intercepto e Inclinação Aleatórios
from pymer4.models import Lmer
modelo_intercpt_inclin_hlm3 = Lmer(formula="desempenho ~ tempo + (tempo|grupo) + (tempo|individuo)", data=df)
modelo_intercpt_inclin_hlm3.fit()
- Modelo Final
from pymer4.models import Lmer
modelo_final_hlm3 = Lmer(formula="desempenho ~ tempo + ativ + texp + ativ:tempo + texp:tempo + (tempo|grupo) + (tempo|individuo)", data=df)
modelo_final_hlm3.fit()
Prevendo...
fixed_result = modelo_final_hlm3.predict(pd.DataFrame({"tempo": [123], "ativ": [456], "texp": [789], "grupo": [0], "individuo": [0]}))
Obervações
- desempemho = variável dependente, o nome é por conta do contexto da aula, desempenho de alunos em escolas.
- ativ = atividade
- texp = tempo de experiência
- tempo = tempo (serie temporal)