Exercícios de Machine Learning Supervisionado
Identificar a variável dependente:
Variável dependente é a variável que queremos prever, ou seja, a variável que queremos explicar. Ela é representada por Y.
- Variável dependente métrica (aderência dos resíduos a normalidade): Modelos de regressão simples e múltipla MQO;
- Variável dependente qualitativa: Modelos de regressão logística binaria e multinomial;
- Variável dependente com valores métricos, discretos e não negativos, para dada exposição (contagem): Modelos de regressão para dados de contagem;
MQO: Mínimos quadrados ordinários
Avaliar 3 pressupostos:
- Aderência dos resíduos a normalidade;
- Multicolinearidade;
- Heterocedasticidade (indicio de variáveis omitidas).;
Desejamos, que os resíduos estejam aderentes a função normal, ausência de multicolinearidade e ausência de Heterocedasticidade. Sendo necessário, podemos aplicar a transformação de Box-Cox na variável dependente para normalizar os resíduos e corrigir algum aspecto do modelos.
Avaliando multicolinearidade
Multiplicação de variáveis independentes, que são correlacionadas, podem causar problemas de multicolinearidade.
Analise do coeficiente de correlação de Pearson entre as variáveis (Matriz de correlação de Pearson);
Se tem variáveis categóricas precisa passar pelo processo de dummizacão.
Avalidando adereência dos resíduos a normalidade
Utilizamos o teste de Shapiro-Francia para avaliar a aderência dos resíduos a normalidade. Se o p-value for menor que a significância, aceitamos a hipótese nula de que os resíduos são normalmente distribuídos.
from statstests.tests import shapiro_francia
teste_sf = shapiro_francia(reg.resid)
alpha = 0.05 # nível de significância do teste
if teste_sf['p-value'] > alpha:
print('Não se rejeita H0 - Distribuição aderente à normalidade')
else:
print('Rejeita-se H0 - Distribuição não aderente à normalidade')
Para fazer a variável dependente se adequar a normalidade, podemos aplicar a transformação de Box-Cox.
Y_boxcox = (Y_i^λ - 1) / λ
Olhar o p-value de cada variável, se for maior que a significância, precisamos remover essas variares (não possuem significância estatística), para isso podemos utilizar o método stepwise. O método stepwise é um método de seleção de variáveis que seleciona as variáveis que mais contribuem para o modelo, entregando o melhor modelo possível.
Pode acontecer qu mesmo depois de aplicar a transformação de Box-Cox, os resíduos não se adequarem a normalidade. Nesse caso, podemos melhorar a base de dados (maior numero de amostras, mais variáveis preditoras relevantes e etc) ou utilizar outros tipos de modelagem (arvores de decisão, redes neurais, etc).
Avaliando Heterocedasticidade
Para avaliar a heterocedasticidade, podemos utilizar o teste de Breusch-Pagan. Se o p-value for menor que a significância, aceitamos a hipótese nula de que os resíduos são homocedásticos.
Heterocedasticidade é a variância dos resíduos que não é constante. Fazendo com que os resíduos sejam mais dispersos em uma parte do gráfico e menos dispersos em outra parte (formato de cone).
A transformação de Box-Cox também pode ser utilizada para corrigir a heterocedasticidade.
Com a transformação de Box-Cox, podemos corrigir a heterocedasticidade e a aderência dos resíduos a normalidade.
Modelos de regressão logística binaria
Modelo de regressão logística binária é utilizado quando a variável dependente é binária (0 ou 1, evento ou não evento).
O cutoff é o ponto de corte que separa as classes da variável dependente em eventos e não eventos. Mudar um cutoff muda a sensitividade, especificidade e acurácia do modelo.
Para avaliar o modelo sem depender do cutoff, podemos utilizar a curva ROC (Receiver Operating Characteristic). A curva ROC é um gráfico que mostra a relação entre a sensitividade e a especificidade do modelo. Para cada cutoff, temos um par de valores de sensitividade e especificidade.
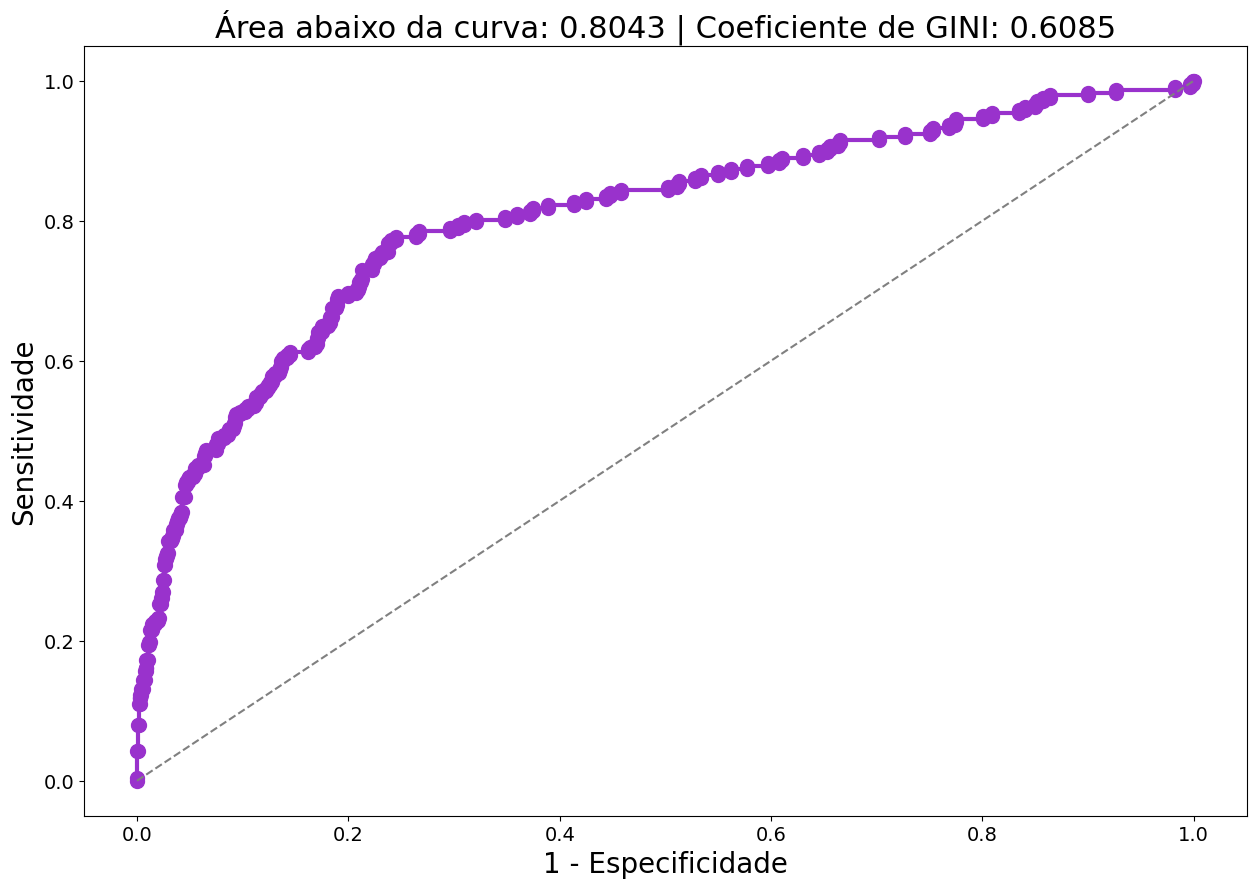
A área sob a curva ROC (AUC) é um indicador da qualidade do modelo. Quanto maior a AUC, melhor o modelo.
A métrica de avaliação de coeficiente de Gini às vezes é utilizada como uma métrica de avaliação alternativa para a AUC e as duas medidas estão estreitamente relacionadas.
O coeficiente de Gini é calculado como o dobro da área entre a curva ROC e a diagonal, ou como Gini = 2AUC – 1.
O odds ratios serve para avaliar a relação entre as variáveis independentes e a variável dependente. O odds ratio é a razão entre a chance de um evento ocorrer e a chance de um evento não ocorrer. Se o odds ratio for maior que 1, a variável independente aumenta a chance do evento ocorrer. Se o odds ratio for menor que 1, a variável independente diminui a chance do evento ocorrer. Podemos saber o quanto a variável independente aumenta ou diminui a chance do evento ocorrer através do odds ratio.
Calculo o predict com todos os valores constantes, exceto em uma categoria, para saber o quanto a variável independente aumenta ou diminui a chance do evento ocorrer através do odds ratio.
chance1 = p1 / (1 - p1)
chance2 = p2 / (1 - p2)
odds_ratio = chance1 / chance2
Então em média a chance de um evento ocorrer é odds_ratio vezes maior ao mudar a variável independente de x para y.
Modelos para dados de contagem
Modelos para dados de contagem são utilizados quando a variável dependente é uma contagem de eventos. Acidentes por semana, número de vendas por dia, número de ligações por hora, etc.
Modelos para dados de contagem são modelos de regressão que se adéquam a distribuição de Poisson ou binominal negativa. Para saber qual devemos olhar para a superdistensão dos dados. Se a variância for maior que a média, utilizamos a distribuição binomial negativa. Se a variância for igual a média, utilizamos a distribuição de Poisson.
- Poisson: Média = Variância
- Binomial Negativa: Variância >> Média
Avaliar também se existe inflação de zeros, que é quando a variável dependente tem muitos zeros. Se a variável dependente tem muitos zeros, podemos utilizar modelos de zero inflado. Para avaliar a inflação de zeros, podemos utilizar a tabela de frequências da variável dependente, para confirmar estaticamente também podemos utilizar o teste de Vuong, que compara o modelo de Poisson com o modelo de zero inflado.
vt = vuong_test(modelo_zip, modelo_poisson)
if vt.pval <= 0.05:
print("H1: Indicates inflation of zeros at 95% confidence level")
else:
print("H0: Indicates no inflation of zeros at 95% confidence level")
Parte dos zeros são estruturais devido ao componente dicotômico da variável dependente, ou seja, a probabilidade de um evento ocorrer ou não o evento.
Separar as variáveis provenientes do componente de contagem e as variáveis provenientes do componente dicotômico.
Comparar o Log-Likelihood de cada modelo, para saber qual é o melhor modelo. Quanto maior o Log-Likelihood, melhor o modelo.
